|
|
|
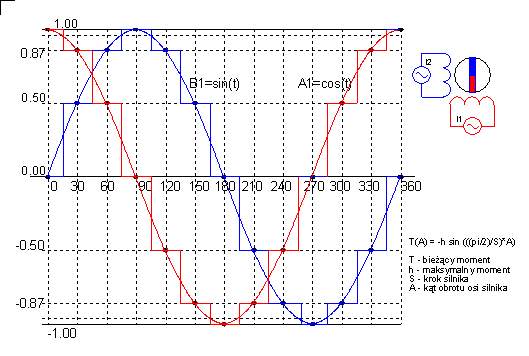
W teorii zakłada
się, że moment trzymający silnika zmienia się w funkcji sinusoidalnej
prądu w uzwojeniu. Pozycja równowagi silnika wyznaczona może być zatem
z porównania wartości prądów w obu uzwojeniach. Jeśli uzwojenia silnika
krokowego pobudzane będą dwoma, przesuniętymi w fazie o 90 stopni napięciami
sinusoidalnymi to ruch silnika będzie płynny i równomierny. W takim sterowaniu
uzyskuje się nieskończoną dokładność sterowania. W praktyce, w układach
cyfrowych stosuje się kwantowanie sygnałów sterujących. Na pokazanym rysunku
pokazano w jaki sposób trzeba sterować silnikiem krokowym z podziałem
pojednyczego kroku na 3 części. Oznacza to, że do sterowania używa się
sygnałów o poziomie odpowiadającym odpowiednio zmieniającym się wartością
funkcji sinus i kosinus dla kątów zmieniających się co 30 stopni. Pełny
okres sterowania elektrycznego wymaga 12 pośrednich stanów przejściowych.
|
|
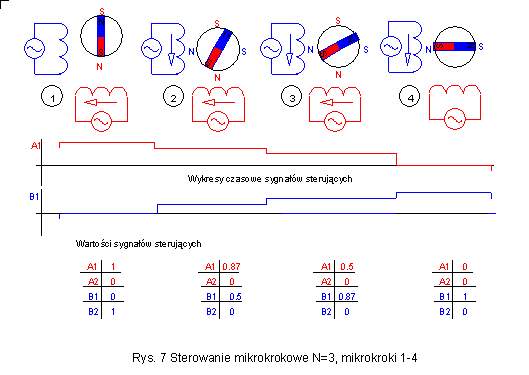
Dla sterowanie mikrokrokowego
prądy w uzwojeniach nie mogą być już jak przy sterowaniu pełno i półkrokowym
kombinacją prądu maksymalnego lub zerowego. Sterowanie mikrokrokowe wymaga
używania prądów mieszczących się pomiędzy wartością amksymalną a zerem.
Na przykładzie sterowania z podziałem kroku na 3 (N=3) części widać, że
do uzyskania prawidłowego sterowania prądy muszą przybierać wartości równe
0.5 oraz 0.87 wartości maksymalnej. |
|
Bez zmian pozostaje
natomiast wymagalność aby znak prądów w obu uzwojeniach pozostawał stale
w odpowiedniej sekwencji. |
|
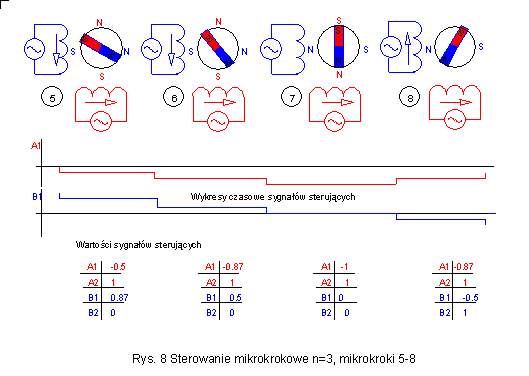
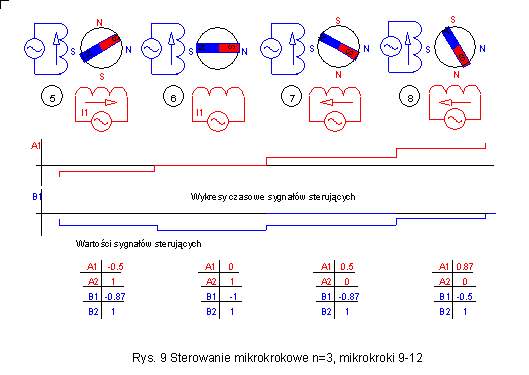
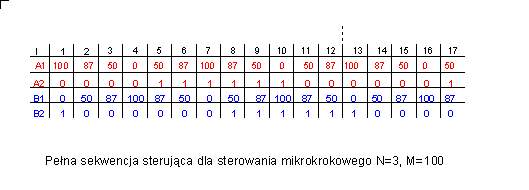
| Dla sterowania z podziałem
kroku podstawowego na 3 części wymagane są 12 stany przejściowe po przebyciu
których powtarza się sekwencja sterująca. W Przechodząc 12 stanów pośrednich
silnik wykona oczywiście 4 pełne kroki podstawowe. |
|
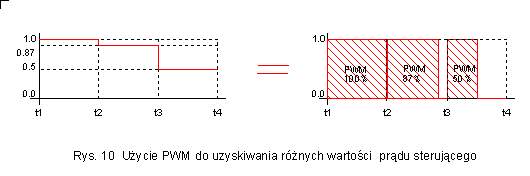
Rysunek 10 pokazuje
w jaki sposób można uzyskać prądy sterujące mieszczące się w zakresie
pomiędzy wartością maksymalną a zerem przy stosowaniu wyłacznie logiki
binarnej. Do uzyskanie dopowiedniego efektu wykorzystuje się tzw modulację
szerokości impulsu (PWM). Na lewym rysunku widać, że prądy o wartości
1, 0.87 i 0.5 utrzymywane są w trakcie trwania równych okresów czasu (t2-1),
(t3-t2) oraz (t4-t3). Biorąc pod uwag efekt energetyczny pokazanych sygnałów
można powiedzieć, że zmienna o wartości 0.5 działająca w czasie (t4-t3)
wywoła podobny efekt jak zmienna o wartości 1 działająca w czasie (t4-t3)/2.
Podobnie zmienna o wartości 0.87 działająca w czasie (t3-t2) wywoła podobny
efekt jak zmienna o wartości jeden działająca w czasie (t3-t2)*0.87. W
ten sposób, kierując czasem działania zmiennej o pełnej wartości w trakcie
trwania impulsu uzyskuje się efekt podobny do użycia wielkości o zmiennej
amplitudzie działającej w ciągu całego czasu trwania impulsu.
Opisane działania uwarunkowane są pewnymi warunkami,
z których najważniejszy polega na tym, że zmiany długości trwania pojedynczego
impulsu sterującego muszą być zbyt szybkie do 'zauważenia' przez sterowany
obiekt, który dostrzega wyłącznie średnią wartość zmian nie mogąc zareagować
na szybko zmieniające się wartości chwilowe. O takich własnie obiektach
mówimy, że są inercyjne dla szybkich sygnałów sterujących. Rzeczywiście
Wirnik silnika krokowego wnosi sporą inercję a uzyskiwane prdkości obrotowe
silników sięgają kilku obrotom na sekundę co odpowiada 5-10 tysięcy mikrokrokom
na sekundę. Sterowanie wypełnieniem impulsu powinno odbywać się zatem
co najmniej 10 razy szybciej a zatem z prędkościami rzędu 100 tysięcy
i więcej zmian w ciągu sekundy. |
|
| Teraz w procedurze
sterowania ważne są wszystkie wartości jakie powinna przyjmować zmienna.
Aby mogła ona przybierać wartości z pewną dokładnością należy założyć podział
podstawowego impulsu sterującego na znacznie mniejsze jednostki. Zakładając,
że jeden impuls sterujący podzielimy na K części można powiedzieć, ze impuls
o wartości 0.87 wartości maksymalnej powinien trwać K*0.87 elementarnych
jednostek. W tabeli wyliczono odpowiednie wielkości dla założenia, że K=100.
Pełna sekwencja sterująca ma 12 stanów pośrednich a wypełnienie impulsu
sterującego wynosi od 100% przez 87%, 50% do 0%. |
|
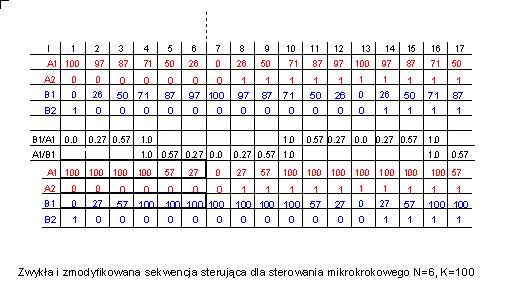
| Przy sterowaniu z
podziałem kroku podstawowego na mniejsze części długość sekwencji sterującej
się wydłuża. Dla przykładu w tabeli podano wartości pierwszych 17 kroków
sekwencji z podziałem kroku podstawowego na 6 części (N=6). Dla takiego
sterowania pełna sekwencja elektryczna ma długość 24. Górne wiersze tabeli
zakładają zmianę prądu sterowania zgodnie z wartościami jakie przybierają
odpowiednio funkcje sin i cos. W środkowej części tabeli znajdują się wyliczenia
proporcji wzajemnych wartości A(I) oraz B(I). Wykorzystując fakt, że położenie
wirnika zależy od stosunku prądów w uzwojeniach można uprościć sekwencję
sterującą zakładając dla jednej z wartości stały poziom sygnału równy 100
jednostek (PWM =100%) i odpowiednio podnosząc wartość drugiego z sygnałów.
W ten sposób np. dla kroku I=3 wartości sterowania wynoszą odpowiednio:
A1(3)=87 (PWM=87%), B1(3)=50 (PWM=50%) i należy zastosować dla obu sygnałów
impulsy wypełnione odpowiednio w 87 i w 50 procentach. Ale jednocześnie
wzajemny stosunek wielkości A1(3) i B1(3) wynosi 0.57. Jeśli więc zmienna
A1(3) równać się będzie 100 (PWM=100%) to zmienna B1(3) powinna mieć wartość
57 (PWM=57%) co zapewni, że pozycja wirnika będzie identyczna. Przez taką
manipulację uzyskuje się 2 efekty: jednym z nich jest zwiększenie momentu
silnika, bo steruje się go zawsze prądem o maksymalnej wartości w co najmniej
jednym z uzwojeń, po drugie upraszcza się sekwencję sterującą bo musi ona
zawierać tylko 4 wartości a nie jak poprzednio 7 wartości. Taka uproszczona
sekwencja wyróżniona została pogrubioną ramką. Sekwencja ta powtarza się
w różnych miejscach okresu sterowania elektrycznego i dla przykładu sekwencja
dla zmiennej B1 z zakresie od I=1 do I=6 powtarza się dla zmiennej A2 od
I=7 do I=12. Realizując algorytm sterowania można pójść dwiema drogami.
Można użyć pełnej tabeli sterowania dla danego podziału kroku podstawowego
na N mikrokroków co skutkuje koniecznością budowania tabel o długościach
N*4 albo można zastosować metodę używania podstawowej sekwencji o długości
równej N dopasowywanej do miejsca w cyklu kroku elektrycznego. Pierwszy
sposób wymaga większej pamięci, drugi szybszego procesora bo ilość operacji
związanych z dopasowaniem sekwencji zwiększa się. Stała pozostaje konieczność
wykonania wszystkich N*4 sekwencji sterujących z tabel A1 i B1 oraz zachowanie
znaków sygnałów sterujących z tabel A2 i B2. |
|